EVALUATION DES RESSOURCES ET SAVOIRS

Exercice 1 : Applications directes du cours

1.  Un objet réel  AB  est placé à  2cm  devant une lentille divergente de distance focale  f’=-2 cm.

Déterminer par construction géométrique la position de l’image  A’B’. 

Déterminer, en utilisant les relations de conjugaison, la position de l’image  A’B’ et le grandissement.

2. Un objet virtuel AB est situé dans le plan focal image d’une lentille convergente de focale  f’=2cm.

Déterminer par construction géométrique la position de l’image A’B’. 

Déterminer, en utilisant les relations de conjugaison, la position de l’image A’B’ et le grandissement.  

3.  A l’aide d’une lentille convergente, on regarde un  objet très éloigné. Le pied de cet objet peut être considéré sur l’axe optique de la lentille. Le sommet de cet objet est vu à l’œil nu sous un angle α =10 °. L’image obtenue sur un écran a une hauteur de 8 cm. Quelle est la distance focale de la lentille utilisée ?

4.  Comment peut-on obtenir simplement un système optique convergent, de distance focale 10cm, en partant d’une lentille divergente de distance focale  -6cm ?

5.  Un doublet est constitué de l’association de deux lentilles minces convergentes de distances focales 15cm et 10cm. Les centres optiques sont distants de  25cm. Montrer que ce système est afocal et déterminer son grandissement angulaire.

6.  Un doublet est constitué de l’association de deux lentilles minces convergentes de distances focales 15cm et 10cm. Les centres optiques sont distants de  5,0 cm. Déterminer, graphiquement  puis en utilisant les relations de conjugaison, la position des foyers du doublet.

Exercice 2 :

1 : Projection d’une image avec une lentille convergente.(**)

1.  Rechercher la distance minimale objet réel - image réelle à l’aide d’une lentille mince convergente.

2.  Méthode focométrique de Bessel et Silbermann :

Un objet  AB  et un écran  (E) sont fixes et distants de  D. Entre l’objet et l’écran, on déplace une lentille mince convergente de distance focale image f’. Montrer que si   f’ ≥ 4D, il existe deux positions de la lentille convergente, distante de d, pour lesquelles il y a une image nette sur l’écran. Exprimer f’ fonction de  D  et  d.

3 : Projection d’une diapositive. (*)

On veut projeter sur un mur, l’image d’une diapositive,  24 mm × 36 mm, à l’aide d’une lentille de distance f' = ±5 cm.

1.  Préciser sa nature convergente ou divergente ?

2.  Si l’écran est à  5m de la lentille, préciser la position de la diapositive le grandissement et les dimensions de l’image.

3.  En ne touchant plus à la distance  D  de la diapositive à l’écran, montrer qu’il existe une autre position de la lentille où l’image est nette. Calculer le nouveau grandissement.

Exercice 3 : Lentilles accolées. (*)

Déterminer la nature, la vergence et la distance focale d'une lentille  L₂  qui, accolée à une lentille convergente L₁  de  75cm  de distance focale, donnerait d'un objet réel et pour une seule position du système  {L₁, L₂}, une image nette sur un écran placé à D = 4 m  de l'objet.

Exercice 4 :

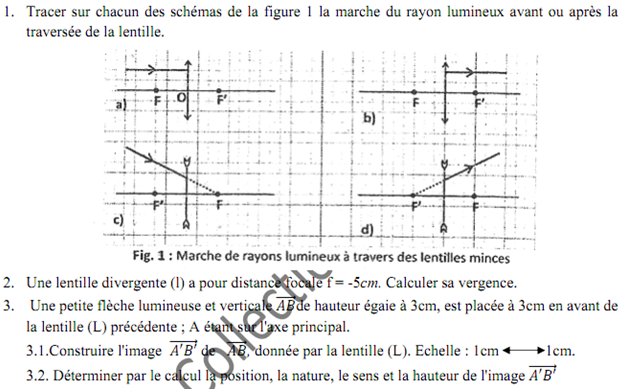
1-1-/ Tracer sur chacun  des schémas de  la figure 1 du document annexe,  la marçhe du  rayon  lumineux incident ou émergent de  la  lentille.  1pt

1-2-/ Une  lentille  (L) divergente a pour distance focale r =  -25,0 cm. Calculer sa vergence.  O,5pt

1-3-1  Un  objet  lumineux  et  vertical  ABde hauteur égale  à  10,0  cm  est  placé  à  15,0  cm  en  avant  de  la lentille  (L)  précédente, A est sur l'axe optique.

1-3-1-1  Construire  sur  la  figure  2  de  l'annexe,  à  l'échelle  1/5,  l'image  A'B'de  AB,  donnée  par  la lentille (L).     1pt

1-3-4-/ Déterminer par calcul,  la position,  la nature,  la hauteur et le sens de  l'image  A' B'.  1,5pt

Exercice 5 :

I-Définir: centre optique; foyer secondaire.  0,5x2=1pt

2-Une lentille donne d'un objet virtuel situé à 30cm de son centre, une image virtuelle située à 60cm du même centre.

2·1. Calculer sa distance focale.  0,5pt

2-2. Calculer son rayon de courbure sachant qu'elle est plane concave d'indice n=1,5.  0,5pt

3. Une lentille mince, de centre optique 0, donne d'un objet réel constitué par une flèche  lumineuse de longueur AB =  3 cm, normal à l'axe principal de  la lentille, une image A'B' sur un écran E. A et A' sont sur l'axe. OA = 40 cm; OA' = 160 cm.

3.1. Quelle est la nature de la lentille? Calculer sa distance focale.  (0,25+0,5)pt

3.2. Construire l'image NB' et déterminer sa taille?  (0,75+0,5)pt

4· Sur un banc  d'optique, on place un  objet AB = 2,5 cm, une  lentille L et un écran E. L'objet AB étant fixe, on déplace  la  lentille L parallèlement à elle-même et on  recueille par déplacement sur l'écran  l'image réelle A₁B₁ , Les positions de A et de A₁ par rapport à 0  sont reportées dans le  tableau suivant.

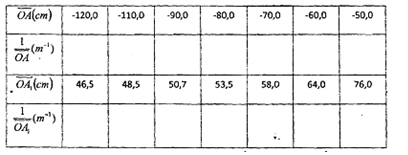
4-1.compléter le tableau et représenter graphiquement en fonction de sur un papier millimétré. Echelle: 1 cm   0,2 m  .                                                               (l,75+1,5=3,25pt

4-2.  En déduire la distance focale f de la lentille L.                                                        0,75pt

Exercice 6 :

1. Soit une lentille de distance focale f’= -3 cm. Trouver graphiquement les caractéristiques de l’image d’un objet réel de taille 2 cm situé à 5 cm du centre optique. (Echelle 1/1).     1.5pt

2. On peut assimiler l’objectif d’un appareil photographique à une lentille mince convergente de distance focale f’= 10 cm.

a- Calculer la vergence de cette lentille.

b- Quelle doit être la distance entre la lentille et le film sensible lorsqu’on photographie avec cet appareil des objets situés à l’infini.

c- Deux points A et B placés à 100 m de cet appareil ont des images A’ et B’ sur le film sensible séparées de 20 mm. Quelle est la distance qui les sépare ?

Exercice 7 :

Exercice 8 :

1-Définir : Lentille ; foyer principal image.

2/ Les schémas ci-dessous représentent quatre lentilles minces.

2.1 Nommer chacune de ces lentilles

2.2 Classer ces lentilles en fonction de leur type.

3 / Comment peut-on différencier physiquement une lentille convergente d’une lentille divergente ?

Exercice 9 :

Exercice 10 :

Exercice 11 :

1. Schématiser une lentille biconvexe.

2. Calculer la vergence et la distance focale de cette lentille.

3. Cette lentille donne d’un objet réel, situé à 10 cm de son centre optique, une image réelle située à 20 cm de l’objet. Vérifier les résultats de la question 2.

Exercice  12 :

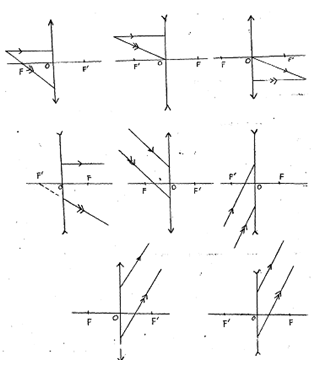
1-1.Déftnir : lentille mince; distance focale; plan focal; foyer secondaire.  0,5x4=:2pts

1'-2. Donner  la représentation symbolique d'une lentille divergente et y placer ses foyers principaux. 

1-3.Donner la différence entre le foyer principal objet et le foyer principal image.  Ipt

1-4 Compléter sur cette feuille le tracé des rayons lumineux dans les différentes figures avec le faisceau émergent ou le faisceau incident. 0.5x8pts

Exercice 13 :

Un objet réel AB de hauteur h = 2cm, est placé à 24 cm devant une lentille divergente de vergence C = -8,33 dioptries, perpendiculaire à l’axe principal.

1.1. Déterminer les caractéristiques de son image A’B’  (nature, position, sens et taille).   1pt

1.2. Faire sur un papier millimétré la construction graphique de A’B’.   1,5pt

Échelle : 1 cm sur le papier équivaut à 3 cm de distance sur l’axe principal et 1 cm équivaut à 1 cm sur l’axe perpendiculaire à l’axe principal.

Exercice 14 :

1)-Une lentille donne d’un objet lumineux de 30 mm de hauteur, situé à 40 cm de son centre optique, une image réelle A’B’ haute de 45 mm.

a)  Quelle est la distance séparant l’écran du centre optique de la lentille ?   Rép. : 60 cm

b)  Quelle est la distance focale de la lentille ?   Rép. : 24 cm

2)-Un objet lumineux AB est situé à 80 cm d’un écran sur lequel on désire projeter une image A’B’ de même taille que l’objet AB.

a)  Quel type de lentille faut-il utiliser ?   Rép. : convergente

b)  A quelle distance de l’objet faut-il placer la lentille ?  Rép. : 40 cm

c)  Quelle doit être la distance focale de la lentille ?   Rép. : 20 cm

Exercice 15 :

Un objet AB de taille 1, 0 cm est placé 5, 0 cm avant le centre optique O d’une lentille convergente, de distance focale f0= 2, 0 cm (AB est perpendiculaire à l’axe optique).

1) Calculer la vergence de la lentille et préciser son unité.

2) Construire l’image A₀B₀ de AB en utilisant les trois rayons «utiles». Mesurer alors A₀B₀ et OA₀.

3) Retrouver OA₀ et A₀B₀ par le calcul.

4) Calculer le grandissement G_t. Que peut-on dire de l’image ?

5) Nommer et rappeler les conditions d’utilisation des expressions précédentes.

EVALUATION DES COMPETENCES

Exercice 2 : Appareil photographique

1. L’objectif d’un appareil photographique est assimilable à une lentille mince convergente (L1) de 10 cm de distance focale. On photographie une tour de 50 m de haut située à 1 km.

(a) À quelle distance de l’objectif se situe l’image A1B1 obtenue ?

(b) Quelle est la taille de cette image ?

2. On associe à cet objectif une lentille mince divergente (L2) de distance focale −4 cm. La pellicule est située à 12 cm de (L2) jusqu’à obtention, sur la pellicule, d’une image finale A′B′ nette.

(a) Quelle est alors la distance O1O2 entre (L1) et (L2) ?

(b) Quelle est la taille de l’image dans ce cas ?

(c) Quel est l’intérêt de (L2) ?

(d) Sur un schéma à l’échelle 1/1, positionner les lentilles (L1) et (L2), les images A1B1 et A′B′ en utilisant les valeurs numériques précédentes. Mettre en évidence sur ce schéma α, l’angle apparent sous lequel on voit l’objet depuis le centre optique de (L1).

(e) Sur le même schéma, tracer la marche, à travers (L1) et (L2), d’un faisceau lumineux incident couvrant toute la lentille (L1) dans les deux cas suivants :

— faisceau parallèle de même direction que l’axe optique du système.

— faisceau parallèle, incliné selon l’angle apparent α.

3. On reprend l’appareil photographique de la question 1.

(a) Quelle devrait être la distance focale d’une lentille convergente unique qui donnerait de la même tour, une image de même taille que celle donnée par le système ((L1),(L2)) précédent ?

(b) Pourquoi utilise-t-on la solution de la question 2. plutôt que celle de la question 3. Pour fabriquer les appareils photographiques ?

Exercice 2 : Etude d’un microscope

Un microscope peut être modélisé par deux lentilles convergentes (L1) et (L2) alignées sur le même axe optique, entourées d’air.(L1) modélise l’objectif et a une distance focale image f′1 = 2 mm. (L2) modélise l’oculaire et a une distance focale image f′2 = 30 mm. La distance ∆ = F′1F2 entre le foyer image de (L1) et le foyer objet de (L2) vaut 160 mm, c’est l’intervalle optique du microscope.

La distance minimale de vision de l’œil est dm = 25 cm (Cf. TP – cours) : c’est le ponctum proximum, la distance au dessous de laquelle l’œil n’arrive plus a accommoder : l’image n’est plus nette.

Par contre, l’œil normal voit net un objet situé à l’infini et cela sans accommoder.

On observe, à travers le microscope, un petit objet AB perpendiculaire à l’axe optique avec A et l’œil sur l’axe optique.

1. Rappeler la formule de conjugaison de Newton pour une lentille mince sphérique.

2. Où doit être placé A pour que l’œil observe AB à travers le microscope sans accommoder ?

Faire l’application numérique.

3. Les deux rayons sortant de la lentille (L2) sur le dessin ci-dessous (qui n’est pas à l’échelle) sont issus de B. Dessiner leur trajet à travers le microscope et trouver ainsi graphiquement la position de AB.

4. Expression du grossissement :

(a) Sous quel angle maximal θ₀ un œil normal voit-il AB sans le microscope ? (on prendra tanθ₀≃θ₀).

(b) Sous quel angle θ l’œil voit-il AB à travers le microscope ? (on prendra tan θ ≃ θ).

(c) On définit le grossissement par G = θ/θ₀. Calculer G en fonction de ∆, dm, f′1 et f′2. Faire l’application numérique.

5. Le cercle oculaire de centre C est l’image de la monture de (L1) à travers (L2).

(a) Que vaut CF′2.

(b) Quel est le diamètre D′ du cercle oculaire sachant que le diamètre de la monture de (L1) est D = 11 mm?

6. Comme la rétine est discontinue, granulaire, l’œil ne peut pas distinguer deux rayons lumineux l’un de l’autre s’ils font entre eux un angle inférieur à ε = 1,5 minute d’arc. Quelle est la taille du plus petit objet AB que l’on pourra distinguer ? On donnera son expression en fonction de ∆, ε, f′

1 et f′2. Faire l’application numérique.

Exercice 3 : Lunette Terrestre « numérique »

On souhaite réaliser une lunette terrestre « numérique ».  On  dispose pour cela de deux lentilles minces L1 et L2 de centre optique O1 et O2, et d'un capteur CCD. Ce capteur a une dimension de 30mmx20mm (horizontal X vertical) et la dimension des pixels qui le constitue est de 16µmx16µm. L’objet que l’on souhaite  imager est un bâtiment de 15m de haut et de 10m de large, situé à 500m. La lentille L1 a une vergence V1=5 dioptries. Pour commencer on ne se sert que de la lentille L1  (objectif de la lunette) et du capteur CCD. L’axe optique du système passe par O1, le centre du capteur CCD et par le centre de l’objet à imager. 

1.  Quelle est la nature de la lentille L1 (convergente ou divergente) ? justifier votre réponse

2.  Calculer la distance focale image   de la lentille L1.

3. A quelle distance de la lentille L1 doit on placer l'écran pour observer une image nette du bâtiment? Expliquez ce résultat.

4.  Quelle la dimension de l'image du bâtiment sur le capteur CCD? L'image est-elle droite ou renversée? Justifiez votre réponse. 

5.  Calculer la taille apparente apparent θv de l’objet dans la direction verticale.

6.  Montrer que l’on peut exprimer la dimension de l’image du bâtiment sur le capteur en fonction de   et de θv. Pour répondre à cette question, aidez-vous d'un tracé de rayon.

Vérifier numériquement.

7.  Donner la dimension du plus petit détail que l’on peut observer sur le capteur CCD.

Etude de l’oculaire

Afin d’obtenir une image un plus grande de l’objet sur le capteur CCD, on utilise la seconde lentille L2. La lentille L2  et le capteur CCD sont situés respectivement à 255mm et à 805mm après la lentille L1.  

1.  Quelle doit être la focale image f2' de la lentille mince L2 pour qui l'image se forme sur le capteur.

2.  Montrer que l’image du bâtiment sur le capteur CCD est trop grande. L'image est-elle droite ou renversée?

3.  A quelle distance la lentille L2 doit se trouver de la lentille L1 pour que les dimensions  de l’image du bâtiment soit égales à celles du capteur. Donner alors la position du capteur CDD par rapport à

L1 qui permet d’observer une image nette.

4.  Quel doit être la distance focale image d’une lentille convergente mince seule qui donnerait la même dimension d’image sur le capteur.

5.  Quel est l’intérêt d’utiliser une association de 2 lentilles plutôt qu’une seule lentille ?