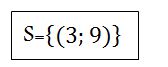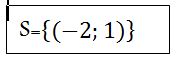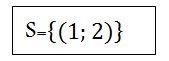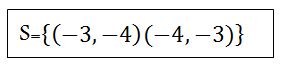Leçon, Résoudre un système d'équations à 2 inconnus avec la méthode de substitution

Correction de l’exercice
Pour les systèmes linéaires, il existe plusieurs manières de résoudre ces systèmes d’équation. Nous allons utiliser la méthode de la substitution. Pour les systèmes contenant les multiplications, nous utiliserons deux méthodes pour que les élèves comprennent mieux.
Commençons avec les systèmes linéaires.
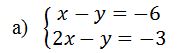
Nous commençons par tirer la valeur de x en fonction de y dans la ligne 1. Cette valeur de x contiendra donc y. Le but est d’isoler un inconnu et de se retrouver seulement avec un inconnu au lieu de deux. x-y=-6 x=-6+y. Nous avons déjà la valeur de x en fonction de y. Bref rappel : Quand un nombre traverse l’égalité ou l’inégalité, il change de signe. C’est pourquoi –y est devenu y.
Une fois que nous avons déjà la valeur de x en fonction de y, nous allons à la deuxième ligne pour remplacer x par sa valeur. Attention ! On ne remplace pas sur la même ligne qu’on a choisie pour exprimer x. On remplace dans l’autre ligne. 2x-y=-3 Nous connaissons déjà la valeur de x, qui est -6+y. On va juste remplacer x de la deuxième ligne par sa valeur. On aura donc ceci : 2(-6+y)-y=-3. A ce niveau, on a plus de x, mais seulement les y. On peut donc facilement développer et tirer la valeur de y. 2(-6+y)-y=-3 -12+2y-y=-3. On les classe en fonction de la ressemblance. On calcule les y à part et on renvoie le-12 après l’égalité, pour le calculer avec le nombre avec lequel il se ressemble, c'est-à-dire -3. Quand il traverse l’égalité, il devient +12. Quand un nombre ou un inconnu traverse l’égalité ou l’inégalité, il change de signe. On a donc ceci : 2y-y=-3+12. On fait le calcul. Pour additionner deux nombres, on prend le signe du plus grand pour mettre au résultat. Si les deux nombres sont de même signe, on fait l’addition. S’ils sont de signes opposés, on fait la soustraction. -3 et +12 sont de signes opposés, on va donc faire la soustraction (12-3). Puisque entre eux le plus grand et 12 et son signe est +, le signe du résultat sera +. On fait pareil avec les y. On a ceci : 2y-y=12-3 y=9.
Nous avons déjà la valeur exacte de y. Ce qui nous reste c’est de trouver celle de x. Et pour le faire, on va à la ligne 1 ou deux, et on remplace y par sa valeur exacte pour trouver x. Faisons-le à la première ligne. x-y=-6 x-9=-6 x=-6+9 x=+3 x=3. Nous avons donc résolu notre système. Mais nous devons présenter le résultat.
|
|
Autre chose. Commencez toujours par écrire x quand vous écrivez la solution, avant d’écrire y après.
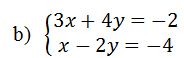
Tirons la valeur de x en fonction de y dans l’équation 1
3x+4y=-2 3x=-2-4y 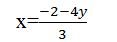
Remplaçons x par sa valeur dans la deuxième ligne
x-2y=-4 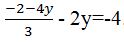 . Ici on
a à faire aux fractions. Tout nombre qui n’a pas de fraction peut se présenter
sous forme de fraction, en ajoutant juste le nombre 1 à son dénominateur. Le
nombre devient le numérateur. 2y peut donc se présenter sous forme de fraction
comme ceci :
. Ici on
a à faire aux fractions. Tout nombre qui n’a pas de fraction peut se présenter
sous forme de fraction, en ajoutant juste le nombre 1 à son dénominateur. Le
nombre devient le numérateur. 2y peut donc se présenter sous forme de fraction
comme ceci : 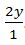 . Notre équation peut donc se présenter comme
ceci :
. Notre équation peut donc se présenter comme
ceci :
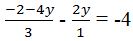 . On va les
réduire au même dénominateur. On fait l’opération. Rappel : Pour
additionner ou soustraire deux fractions, on fait le fameux produit des moyens,
produit des extrêmes, et on multiplie les dénominateurs. Les numérateurs sont
ceux qui sont en haut, et les dénominateurs sont en bas. On va donc multiplier
-2-4y par 1, maintenir le signe de l’opération, multiplier 2y par 3, et enfin
multiplier 3 par 1 (les dénominateurs des deux fractions). On a ceci :
. On va les
réduire au même dénominateur. On fait l’opération. Rappel : Pour
additionner ou soustraire deux fractions, on fait le fameux produit des moyens,
produit des extrêmes, et on multiplie les dénominateurs. Les numérateurs sont
ceux qui sont en haut, et les dénominateurs sont en bas. On va donc multiplier
-2-4y par 1, maintenir le signe de l’opération, multiplier 2y par 3, et enfin
multiplier 3 par 1 (les dénominateurs des deux fractions). On a ceci : 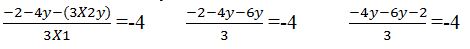 . -4 peut
aussi s’écrire sous forme de fraction. L’équation peut donc s’écrire comme
ceci :
. -4 peut
aussi s’écrire sous forme de fraction. L’équation peut donc s’écrire comme
ceci : 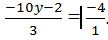 Quand il y a égalité, on fait produit des moyens =
produit des extrêmes. On va multiplier -10y-2 par 1, mettre le signe = et
multiplier 3 par -4. L’équation va donner ceci : -10y-2=-12. A ce niveau
on peut le résoudre plus facilement. -10y = -12+2 -10y =
-10
Quand il y a égalité, on fait produit des moyens =
produit des extrêmes. On va multiplier -10y-2 par 1, mettre le signe = et
multiplier 3 par -4. L’équation va donner ceci : -10y-2=-12. A ce niveau
on peut le résoudre plus facilement. -10y = -12+2 -10y =
-10 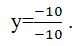 Quand il y a
le signe – au numérateur et au dénominateur, les deux s’annulent. On ne laisse
jamais le signe – au dénominateur. Quand il y a le signe négatif au
dénominateur, on le fait monter au numérateur pour multiplier celui qui s’y
trouve. Dans notre équation, y=1.
Quand il y a
le signe – au numérateur et au dénominateur, les deux s’annulent. On ne laisse
jamais le signe – au dénominateur. Quand il y a le signe négatif au
dénominateur, on le fait monter au numérateur pour multiplier celui qui s’y
trouve. Dans notre équation, y=1.
Remplaçons x par sa valeur dans la deuxième équation.
x-2y=-4 x-2(1)=-4 x-2=-4 x=-4+2 x=-2
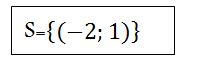
Nous avons pris un long chemin. On pouvait juste aller dans le système d’équation voir la ligne où on pouvait tirer x ou y plus facilement sans arriver aux fractions. Cette ligne était la deuxième ligne. On pouvait traiter l’équation comme ceci :
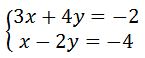
Tirons la valeur de x en fonction de y dans l’équation 2
x-2y=-4 x=-4+2y
Remplaçons x par sa valeur dans l’équation 1
3x+4y=-2 3(-4+2y)+4y=-2 -12+6y+4y=-2 10y-12=-2 10y=-2+12
10y=10 y=1
Remplaçons y par sa valeur dans l’équation 1
3x+4y=-2 3x+4(1)=-2 3x+4=-2 3x=-2-4 3x=-6 x=-2
|
|
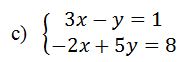
Tirons la valeur de y en fonction de x dans l’équation 1
3x-y=1 -y=1-3x y=-1+3x
Remplaçons y par sa valeur dans la deuxième équation 2
-2x+5y=8 -2x+5(-1+3x)=8 -2x-5+15x=8 -2x+15x=8+5 13x=13 x=1
Remplaçons x par sa valeur dans l’équation 1
3x-y=1 3(1)-y=1 3-y=1 -y=1-3 -y=-2 y=2
|
|
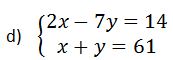
|
Tirons la valeur de x en fonction de y dans l’équation 2 x+y=61 x=61-y Remplaçons x par sa valeur dans l’équation 1 2x+7y=14 2(61-y) -7y=14 122-2y-7y=14 -2y-7y=14-122 -9y=-108 y= 12 Remplaçons y par sa valeur dans l’équation 2
|
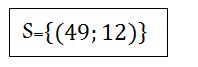
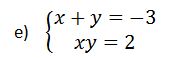
Ce genre de système ne se résout pas de la même manière que les autres. Celui-ci a une multiplication. La LIMARA (Ligue des Masses pour la Renaissance Africaine), la Ligue Associative Africaine et moi vous apprenons deux méthodes pour le résoudre.
Première méthode : somme et produit
La première ligne est une addition. On va l’appeler S pour dire somme. La ligne 2 est une multiplication. C’est donc un produit. On va l’appeler P.
La formule est : X2-SX+P=0
On connait déjà la valeur de S, qui est -3. (x+y=-3). On peut donc, dans notre formule, remplacer S par sa valeur qui est -3.
On connait aussi la valeur de P, qui est 15. (xy=2). On peut aussi remplacer P par sa valeur qui est 2.
On aura donc cette équation : x2-(-3)x+2=0. x2+3x+2=0
On a ici une équation de second degré qu’on peut facilement résoudre.
=b2-4ac 32 – 4(1x2) 9-4(2) 9-8 =1
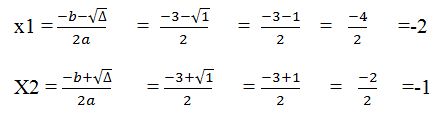
On a donc deux valeurs de x, et aucune valeur de y. On dit juste que si x vaut -1 (x1), y va valoir -2 (x2), et vice-versa. La solution sera donc deux couples. Le couple -1 et -2, et le couple -2 et -1. On écrit comme ceci :
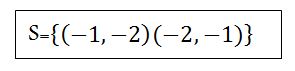
Deuxième méthode : Par substitution
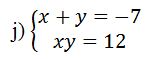
On vient sur la première ligne et on tire la valeur de x en fonction de y
x+y=-7 x=-7-y
On remplace x par sa nouvelle valeur dans la deuxième ligne
xy=12 (-7-y)y=12 -7y-y2=12 -y2-7y-12=0 Nous avons une équation de second degré qu’on peut résoudre avec la méthode du discriminant.
=b2-4ac -72 – 4(-1x-12) 49-4(12) 49-48 =1
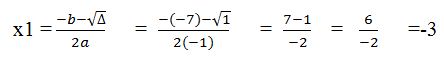
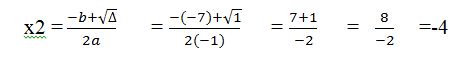
On a donc deux solutions qui sont x1 et x2, mais pas de y. Il nous faut donc trouver les y. Chaque x aura son y pour que le système soit résolu. Bref, pour chaque x, on va chercher son y pour qu’ils soient un couple.
Si x=-3,
Allons à la première ligne. x+y=-7 -3+y=-7 y=-7+3 y=-4. Le premier couple est (-3,-4)
Si x=-4,
Restons sur la première ligne. x+y=-7 -4+y=-7 y=-7+4 y=-3. Le deuxième couple est (-4,-3)
La solution est :
|
|
La LIMARA (Ligue des Masses pour la Renaissance Africaine), la Ligue Associative Africaine et moi, nous vous avons montré comment résoudre les équations à deux inconnus. Nous n’allons pas traiter toute la fiche. Pour le reste de systèmes, nous allons juste donner les réponses. Il est donc mieux de traiter vous-mêmes et vérifier la correction après. Mais toute la correction se détailléee se trouve dans notre site web www.ligueaa.org. Exercez-vous dans notre site web à traiter des centaines d’exeercices sur chaque leçon et sur toutes les matières.
Le combat pour la renaissance africaine continue…
|